Opportunity Costs

Aspiring anonymous math teacher, John Dewey, has filed another report on his latest travails at Ed school. In this report, Dewey sheds some light on the often ignored hidden costs of "discovery learning":

My idea of “discovery” is quite different than his. Take the problem of finding a formula for the sum of interior angles of a convex polygon which we discussed in class. The solution hinges on the fact that the sum of the angles of a triangle = 180 degrees. You could approach teaching this lesson by guided discovery, and show how to split up a quadrilateral and pentagon into triangles to derive the sum of the interior angles. After several minutes of discussion, some students may identify key patterns and the teacher could wrap it up. I suggested this to Mr. NCTM, remarking that it really wasn't giving away the store and there was still some discovery involved.

He nodded acknowledgement but continued to “guide” our class to the constructivist approach: 45 minutes of discovery including having students actually measure the angles of various convex polygons with a protractor, and after accounting for error in measurement, making conjectures and seeing “patterns”. One fellow student asked why one would do that when in fact geometry was about deductive reasoning and learning to reach conclusions about measurement without the aid of actual measurement devices. Mr. NCTM said students should be given free reign to discover the superiority of the deductive method.

For fear of being forever branded as a blog poseur, I hesitate to say whether my approach would be called “direct instruction” or “guided discovery” or Vygotsky’s Zone of Proximal Development and its related term, “scaffolding.” I just offer that the type of discovery my approach entails is what I and others in my age group had growing up. Given a choice between giving students 45 minutes to reach an “aha” experience, or 5 to 10 minutes, I and others like me opt for the latter.

The cost of "discovery learning" is instructional time.

Let's assume that the instructional goal is to convey a particular concept to the students. In Dewey's example the concept was that the sum of the angles of a triangle = 180 degrees. Let's further stipulate that this concept can be adequately conveyed to a student using either a discovery method or a direct instruction method and that in both methods the teacher will attempt to convey the concept with understanding.

Whether the student has actually learned the concept and understands it is easily testable. For example, after the teacher has taught the sum of the angles of a triangle concept and the concept that alternate interior angles of two parallel lines are congruent, the student who understands both concepts should be able to solve for b in the following problem:


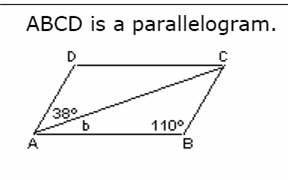Students who can't solve the problem likely do not understand either or both of the taught concepts. In fact, there is a good argument that the concepts have not been "taught" to these students since they have not yet learned the concepts. The effective teacher will go back and reteach the concepts until the students understand them.

The initial learning of the concept is only the first half of the learning process. The second part is retaining the concept in long term memory. This is most efficiently achieved by the student overlearning the concept through practice. Retention is also easily tested by giving a delayed test, say at the end of the course, containing a problem similar to the one given above.

Now let's get back to Dewey's example so we can understand the hidden cost of discovery learning. The sum of the angles concept should be teachable in about 10 minutes of classroom time using either direct instruction alone or some combination of direct instruction and a few minutes of discovery opportunity, as Dewey suggests. In contrast, the guided discovery method, as it is typically practiced in problem-solving/constructivist curricula, might take four times that amount of classroom in order for all the students to discover the concept. In this same period of time, the direct instruction teacher could teach another concept and still have plenty of time left over for the students to practice the concepts they've previously been taught, thus improving their retention.

These are the opportunity costs associated with the discovery learning pedagogy. The opportunity to learn more quickly through more efficient forms of instruction and the opportunity to practice what you've already learned.

The counterargument you most often hear from discovery learning proponents is that students understand the material better if they construct the knowledge for themselves. This might be a legitimate argument if it were true, but so far it remains unproven. Kids who learn via discovery learning are not demonstrating their superior understanding in simple skills tests like the example I've given or, for that matter, in any demonstration or test that supposedly tests higher order thinking skills, whatever they might be.